I tried punching in 243 and it gave me an equation that resolves to 235.

https://www.wolframalpha.com/input?i=(lim+((x^2-100)%2F(x%2B10))%2C+x->13)^5+-+([lim((e^(8x)-1)%2Fx)%2C+x->0]+-+[[lim+((x^2-36)%2F(x-6))%2Cx->-5]+-+lim(cos^2+x+%2B+sin^2+x)%2C+x->36])

Tried it a few other times and it seems to sometimes like giving something that results in 3^5 (which would be 243 on its own) followed by subtracting a bit from it, which ends up making it the wrong answer. In the link above, it basically goes (3^5) - (8 - (1 - 1)), so if you only keep the first brackets it would be correct.

It’s good, although I expected something like the following that I wrote in the past:

In this formula, the subscript 36 refers to the radix 36, so it means that both the polynomial coefficients as well as its roots are base-36; all Latin letters are base-36 digits and that’s why I used a Greek letter as the variable for the polynomial; it has two roots holding a humorous yet deep meaning.

Decimal version (convert the two roots to base-36):

f(x) = x^2 - 18425439x + 11126047267730

I think this would be a lot cooler if there was a complexity modificator to make the solution appear as cryptic as now, but easier to solve for average people.

Rdrr funny guy.

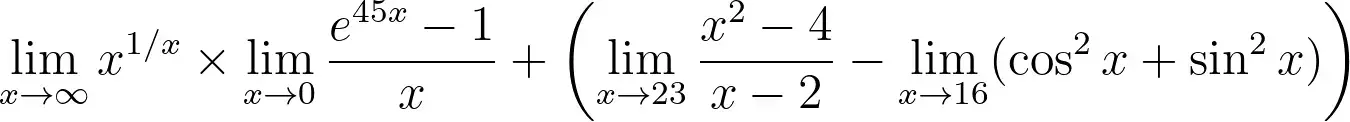
Huh, I don’t think they’ll be able to know what number it’s supposed to be…